 En cartographie, une courbe isochrone est une courbe géométrique délimitant les points accessibles par un véhicule – terrestre ou aérien – en un temps donné (par exemple, la zone pouvant être desservie en moins de 30 minutes par un livreur de pizza ou un dépanneur de matériel informatique).Ou bien en distance parcourue dans ce cas précis on parle d’Isodistance.
En cartographie, une courbe isochrone est une courbe géométrique délimitant les points accessibles par un véhicule – terrestre ou aérien – en un temps donné (par exemple, la zone pouvant être desservie en moins de 30 minutes par un livreur de pizza ou un dépanneur de matériel informatique).Ou bien en distance parcourue dans ce cas précis on parle d’Isodistance.
1. Objectif
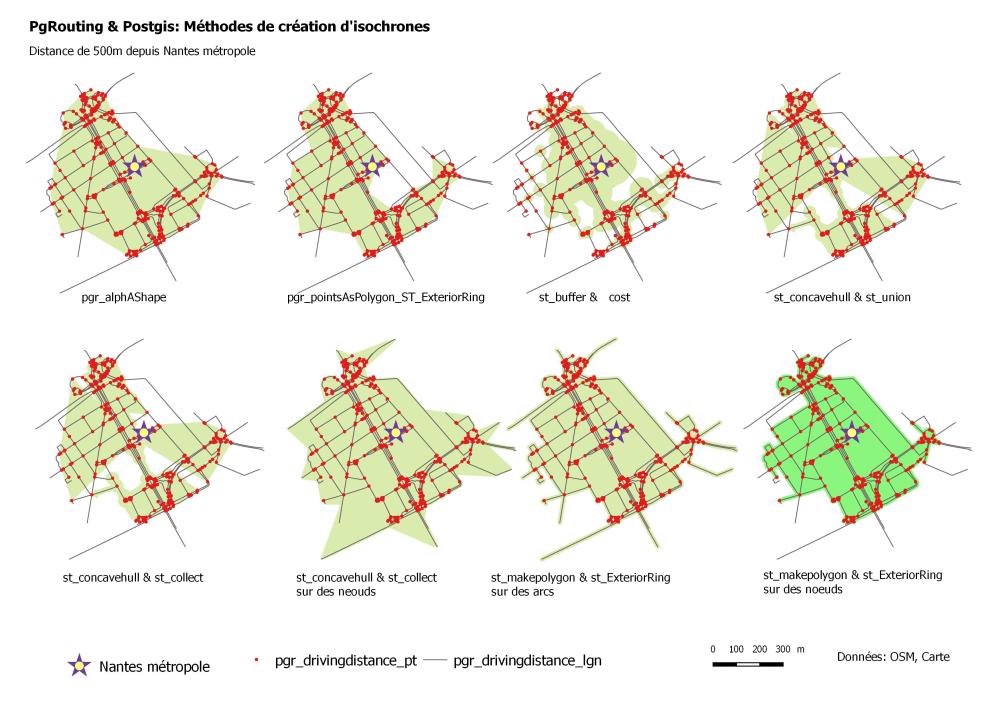
Analyse comparative d’Isodistances de 500m à depuis de Natntes métropole.
2. Méthodes de création d’isochrones
D’abord, pour créer une structure topologique complète et vous familiariser avec pgrouting, je vous renvoie à l’article précédente dans cette page: https://diouck.wordpress.com/postgispgrouting/
Après avoir modéliser notre réseau, nous allons calculer et visualiser les nœuds et arcs qui se situent à 500m de Nantes métropole. Pour ce faire nous allons utiliser l’algorithme driving distance de pgRouting pour calculer la distance la plus coute accessible à moins de 500m.
ØDriving distance pour les nœuds --Drop table routing.pgr_drivingdistance_pt; create table routing_nantes.pgr_drivingdistance_pt as SELECT id1 AS node_id , cost,geom FROM pgr_drivingdistance( 'SELECT edge_id as id, start_node as source, end_node as target, tps_distance as cost from routing.edge_data', 12616, 0.5, false, false ) as di JOIN routing.node pt ON di.id1 = pt.node_id; Ø Driving distance pour les tronçons --Drop table routing.pgr_drivingdistance_lgn; create table routing_nantes.pgr_drivingdistance_lgn as SELECT id1 AS node_id ,pt.tps_distance as cost,geom FROM pgr_drivingdistance( 'SELECT edge_id as id, start_node as source, end_node as target, tps_distance as cost from routing.edge_data', 12616, 0.5, false, false ) as di JOIN routing.edge_data pt ON di.id1 = pt.start_node;

Comme vous pouvez le constater les deux résultats sont légèrement différents.
Les nœuds retournent exactement la distance entre 0 et 499m
tandis que les arcs(tronçons de voirie) dépassent de plusieurs mètres sur les extrémités.
Cette erreur est liée aux intersections entre les nœuds extrêmes et les arcs qui les touches au-delà des 500m. Maintenant nous allons comparer différents isodistances à partir des nœuds et des arcs et voir lesquels s’approchent le mieux à la réalité.
a- Isodistance avec la fonction pgr_alphAShape
Cette fonction retourne un tableau avec des lignes (x, y) qui décrivent les sommets d’une forme alpha. Nous allons donc le coupler avec l’algorithme de driving distance pour créer un polygone à partir des sommets des nœuds et des arcs. Pour plus d’information je vous renvoie vers cette documentation:
A Closer Look at Alpha Shapes in pgRouting
--DROP TABLE routing.isochrone_pgr_alphAShape
CREATE TABLE routing.isochrone_pgr_alphAShape AS
SELECT ST_MakePolygon(ST_AddPoint(foo.openline, ST_StartPoint(foo.openline)))::geometry, 2 as alphaPoly
from (select st_makeline(points order by id) as openline from
(SELECT st_makepoint(x,y) as points ,row_number() over() AS id
FROM pgr_alphAShape('SELECT node_id::integer as id, st_x(geom)::float as x, st_y(geom)::float as y FROM routing.pgr_drivingdistance_pt')
) as a) as foo;

L’Isodistance regroupe bien les sommets des nœuds pour créer un polygone. Cependant on peut constater une légère surestimation des distances.
b- Isodistance avec la fonction pgr_pointsAsPolygon
Comme la fonction précédente, elle va créer un polygone plus précis au tour des nœuds.
--DROP TABLE routing.pgr_pointsAsPolygon; CREATE TABLE routing.pgr_pointsAsPolygon AS SELECT 500, ST_SetSRID(geom,2154) FROM pgr_pointsAsPolygon( 'SELECT node_id::integer as id, st_x(geom)::float as x, st_y(geom)::float as y FROM routing.pgr_drivingdistance_pt') as geom;
On Remarque une très grande précision sur les noeuds. Mais il sous-estime l’emprise des noeuds. Essayons maintenant de fermer le polygone ouvert à l’intérieur.
--DROP TABLE routing.pgr_pointsAsPolygon_ST_ExteriorRing; CREATE TABLE routing.pgr_pointsAsPolygon_ST_ExteriorRing AS with pgr_pointsAsPolygon as ( SELECT 500, ST_SetSRID(geom,2154) as geom FROM pgr_pointsAsPolygon( 'SELECT node_id::integer as id, st_x(geom)::float as x, st_y(geom)::float as y FROM routing.pgr_drivingdistance_pt') as geom ) SELECT ST_MakePolygon(ST_ExteriorRing(ST_GeometryN(geom,1))) as geom FROM pgr_pointsAsPolygon;
c- Isochrone avec St_buffer sur les coûts (distance)
L’objectif est de pondérer les coûts en fonction de la distance. Cette méthode est inspirée de cet article http://anitagraser.com/2013/07/07/public-transport-isochrones-with-pgrouting/
--Isochrones à partir de buffer drop table routing.buffer_cost; CREATE TABLE routing.buffer_cost as with buffer as ( select case when cost<1 then (0.5-cost)*200 end as cost,geom from routing.pgr_drivingdistance_pt) select st_union(st_buffer(geom,cost)) as geom from buffer ;
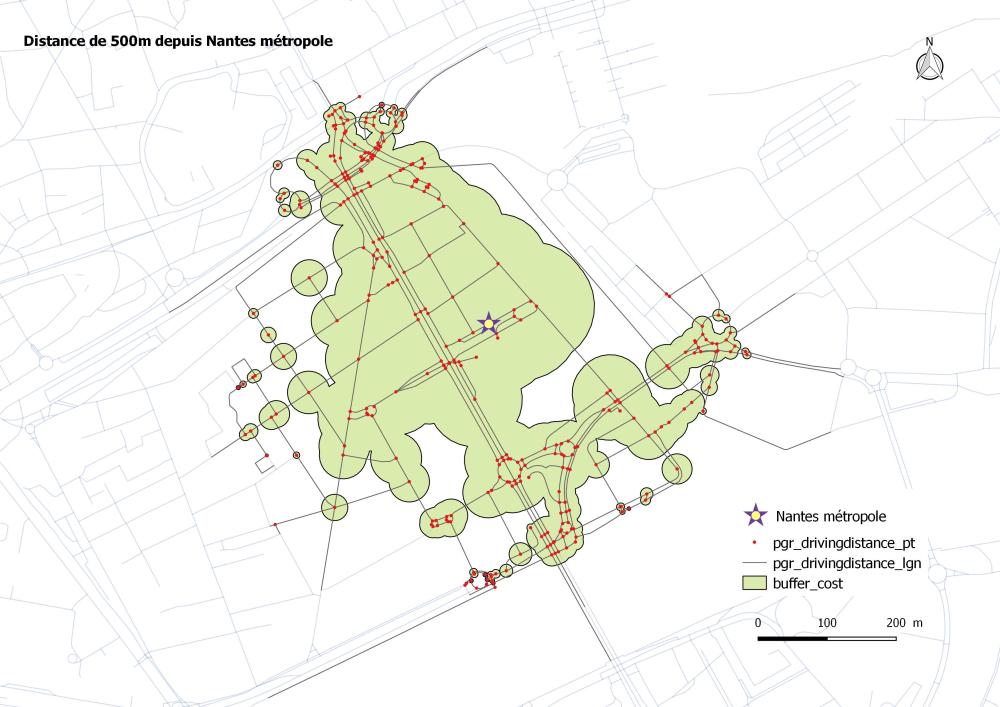 Il faudra adapter la requête. La méthode est bonne mais on remarque qu’en même des discontinuités spatiales. Nous avons des zones discontinues et inaccessibles alors qu’en réalité elles devraient l’être.
Il faudra adapter la requête. La méthode est bonne mais on remarque qu’en même des discontinuités spatiales. Nous avons des zones discontinues et inaccessibles alors qu’en réalité elles devraient l’être.
d- Isochrone avec st_concavehull et st_union
Cette méthode va nous permettre de créer une enveloppe concave autour d’un nuage de points (concave hull). Pour plus d’information je vous renvoie vers la documentation compète :
http://www.portailsig.org/content/sur-la-creation-des-enveloppes-concaves-concave-hull-et-les-divers-moyens-d-y-parvenir-forme
drop table routing. st_concavehull_st_union; CREATE TABLE routing. st_concavehull_st_union as SELECT 1 AS id, st_concavehull(st_union(t.geom), 0.7)--ST_ConcaveHull(ST_Collect(geom),0.95,true) -- FROM (SELECT seq, id1 AS node, id2 AS edge, cost, pt.geom FROM pgr_drivingdistance( 'SELECT edge_id as id, start_node as source, end_node as target, tps_distance as cost from routing.edge_data', 12616, 0.5, false, false ) AS di JOIN routing.node pt ON di.id1 = pt.node_id) t;

Vous pouvez modifier la précision à votre guise. Ici elle est de 0.7. L’isochrone reste correct mais imprécis avec quelques imperfections.
e- Isochrone avec St_ ConcaveHull et st_Collect
La méthode inspirée de ce poste :
http://gis.stackexchange.com/questions/95771/creating-isochrones-in-postgis-osm2po-pgrouting-and-then-saving-the-isochrones-a
La tolérance optimale se situe à 0.7. Vous pouvez évidemment l’adapter à vos besoins.
Avec les arcs
drop table routing.ST_ConcaveHull_ST_Collect_lgn;
create table routing.ST_ConcaveHull_ST_Collect_lgn as
SELECT ST_ConcaveHull(ST_Collect(geom),0.70,false)
FROM routing.edge_data
JOIN (SELECT * FROM pgr_drivingdistance('
SELECT edge_id as id, start_node as source, end_node as target, tps_distance as cost from routing.edge_data',
12616, 0.5, false, false ))
AS route
ON routing.edge_data.start_node = route.id1 ;
Avec les noeuds
drop table routing.ST_ConcaveHull_ST_Collect_pt;
create table routing.ST_ConcaveHull_ST_Collect_pt as
SELECT ST_ConcaveHull(ST_Collect(geom),0.70,false)
FROM routing.edge_data
JOIN (SELECT * FROM pgr_drivingdistance('
SELECT edge_id as id, start_node as source, end_node as target, tps_distance as cost from routing.edge_data',
12616, 0.5, false, false ))
AS route
ON routing.edge_data.start_node = route.id1 ;
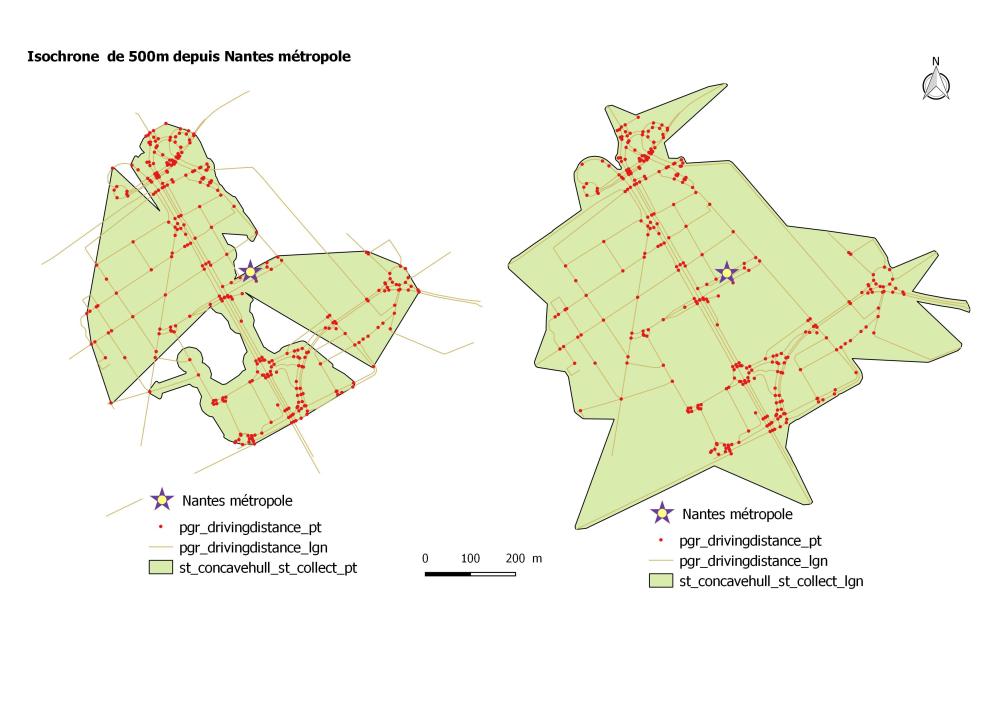
On a soit une surestimation liée aux intersections avec les nœuds externes sur les arcs de plus 500m ou une sous-estimation du polygone créé.
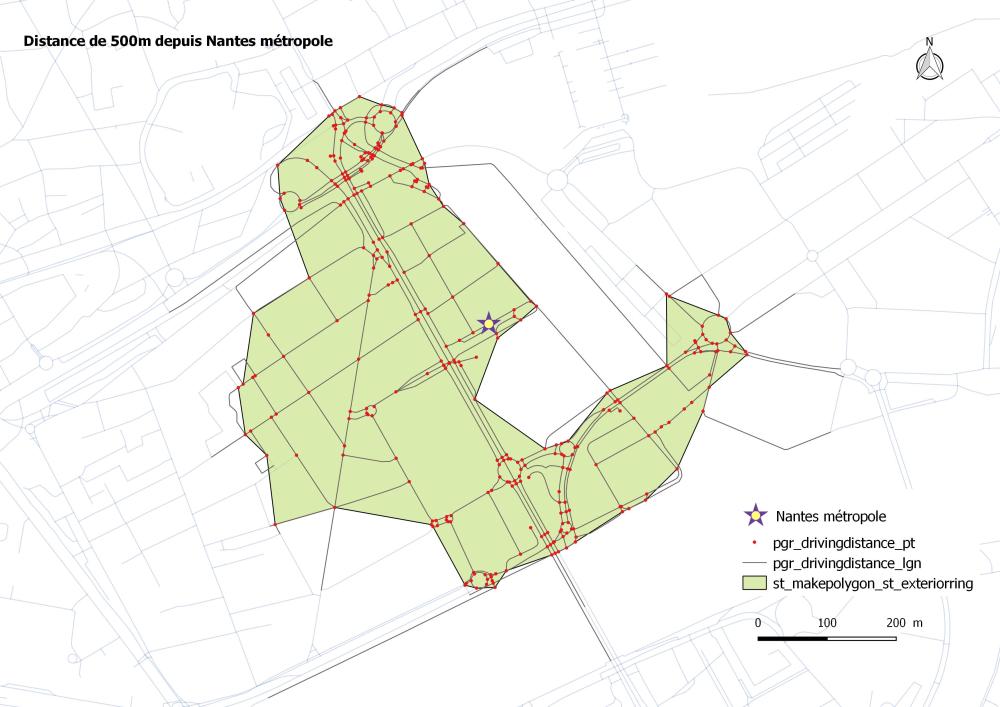
f- Isochrone avec ST_MakePolygon et ST_ExteriorRing
Objectif: nn ferme les polygones après un buffer pour créer un polygone unique.
Avec les arcs drop table routing.ST_MakePolygon_ST_ExteriorRing; create table routing.ST_MakePolygon_ST_ExteriorRing as WITH buffer_itineraire as ( SELECT --id1 AS node_id ,pt.cost, st_buffer(st_union(geom),10 ) as geom FROM pgr_drivingdistance( 'SELECT edge_id as id, start_node as source, end_node as target, tps_distance as cost from routing.edge_data', 12616, 0.5, false, false ) as di JOIN routing.edge_data pt ON di.id1 = pt.start_node) ---Fermer les polygones SELECT ST_MakePolygon(ST_ExteriorRing(ST_GeometryN(geom,1))) as geom FROM buffer_itineraire; Avec les arcs et les noeuds drop table if exists routing. ST_MakePolygon_ST_ExteriorRing_v2; create table routing. ST_MakePolygon_ST_ExteriorRing_v2 as with buffer_itineraire as ( SELECT et.edge_id , st_buffer(et. geom,10, 'endcap=square join=round') as geom , 1 as factor FROM (SELECT id1,cost from pgr_drivingDistance( 'SELECT edge_id as id,start_node as source , end_node as target, tps_distance as cost FROM routing.edge_data', '12616','0.5',false,false) ) firstPath CROSS JOIN (SELECT id1,cost from pgr_drivingDistance( 'SELECT edge_id as id,start_node as source , end_node as target,tps_distance as cost FROM routing.edge_data', '12616','0.5',false,false) ) secondPath INNER JOIN routing.edge_data et ON firstPath.id1 = et.start_node AND secondPath.id1 = et.end_node) SELECT ST_MakePolygon(ST_ExteriorRing(ST_GeometryN(st_union(geom),1))) as geom FROM buffer_itineraire;
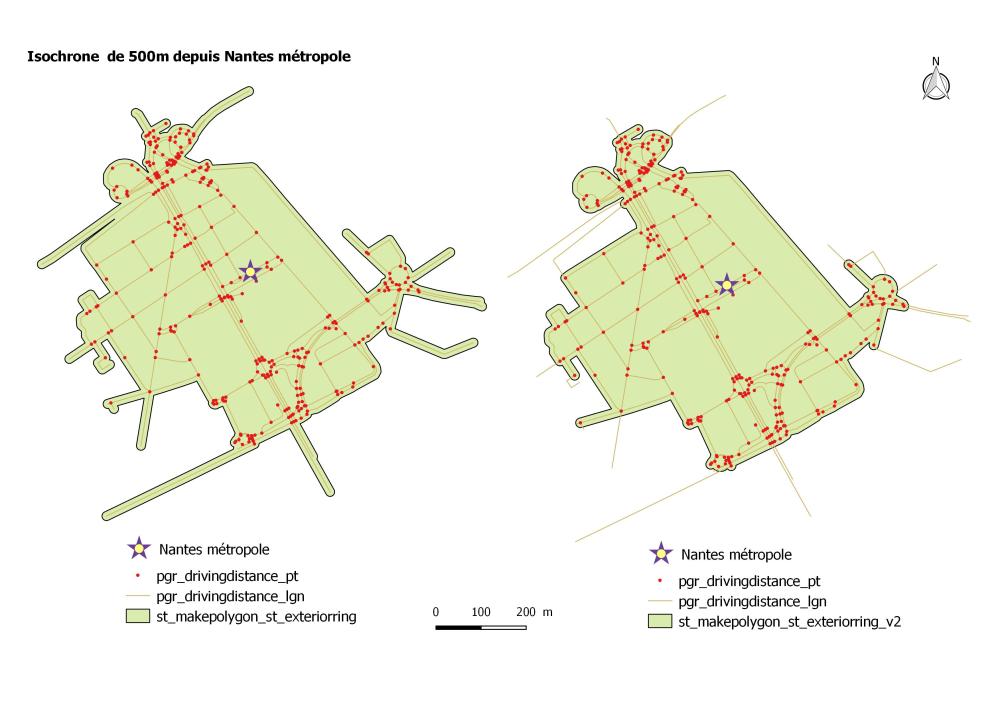
Ce sont les polygones qui s’approchent mieux de la réalité et en particulier l’isochrone avec les nœuds.
g- Synthèse
L’objectif était de voir comment créer un isochrones. Il existe comme vous pouvez le constater plusieurs façons d’y arriver. Les méthodes sont à adapter en fonction de vos besoins. L’isochrone qui se rapproche le plus de la réalité dans cette exercice est celle que j’ai optimisé avec un ST_MakePolygon couplée de ST_ExteriorRing sur les nœuds et non sur les troncons du réseau de voirie de Nantes métropole.
A suivre prochaine étapes les isochrones sachant qu’on peut opérer de la même façon pour comparer l’accessibilité d’un lieu en minutes ou heures.

2 commentaires Ajouter un commentaire